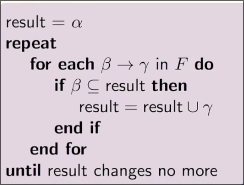Attribute Closure (Relational Algebra)

relational-algebra

Definition

Attribute Closure (Relational Algebra)

Let $\mathcal{R}$ be a schema of a relation $R$ and $\alpha \subseteq \mathcal{R}$ (subset of attributes of $\mathcal{R}$).

The attribute closure ${\alpha }^{+}$ w.r.t. a set of functional dependencies $F$ is the set of attribute which are functionally determined by $\alpha$:

$${\alpha }_F^{+}=\{A\mid \left(\alpha \to A\right)\in F^{+}\}$$

Example: $\alpha \to \beta \in F^{+}⟹\beta \in {\alpha }_F^{+}$

Algorithm