Coding Theory

coding-theory

Definition

Coding Theory

Coding Theory refers to the theory of error-correcting and -detecting codes.

Goals

• Data Compression: Reduction of data volume
• Coding Theory: Protection against transmission errors (through increased redundancy)
• Cryptography: Protection against unwanted receivers and transmitters

Redundancy

Redundancy

Redundancy means including information that can be removed without losing the original data.

Multilevel Coding

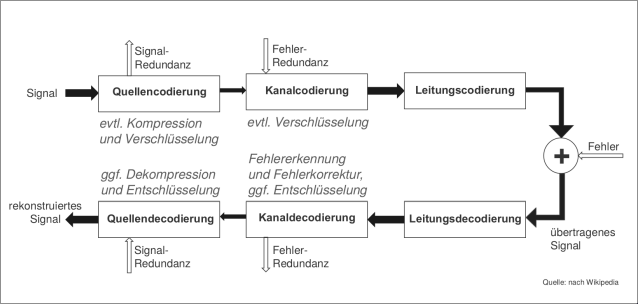
• Source Coding: Original data is encoded using binary numbers (e.g. compression or encryption)
• Channel Coding: Re-coding of the binary data (e.g. compression or encryption)
• Line Coding: Re-coding of data to optimise it for the transmission medium

Error Detection and Correction

Errors always occur when information is transmitted, e.g. when calling someone on the phone. To reduce errors, redundancies are introduced.

Types of Transmission Errors

There are two major types of transmission errors:

• Single Bit Errors: A single bit or multiple unrelated bits are disturbed.
• Bursts: Multiple consecutive bits are disturbed.

Shannon Information

Relative Frequency

The relative frequency of a symbol $x$ is given by:

$$p=\frac{n_x}{n}$$

where $n_x$ is the number of occurrences that a symbol occurs in a word $n$.

Information Content

The information content is given by:

$$h={\log }_2\left(\frac{1}{p}\right)={\log }_2(p^{-1})=-{\log }_2(p)$$

where $p$ is the relative frequency of a symbol.

Entropy (Average Information Content)

Let $\mathcal{I}$ be the set of symbols, then the entropy $H$ is given by:

$$H=\sum _{i\in \mathcal{I}}{p}_i\cdot h_i=\sum _{i\in \mathcal{I}}{p}_i\cdot {\log }_2\left(\frac{1}{p_i}\right)=-\sum _{i\in \mathcal{I}}{p}_i\cdot {\log }_2(p_i)$$

Example: Compute the entropy of the following alphabet:

	$p_i$	$h_i$
$x$	$0.5$	$1$
$y$	$0.25$	$2$
$z$	$0.25$	$2$

Then $H$ is:

$$H=\underset{\text{w.r.t.}x}{\underbrace{0.5\cdot 1}}+\underset{\text{w.r.t.}y}{\underbrace{0.25\cdot 2}}+\underset{\text{w.r.t.}z}{\underbrace{0.25\cdot 2}}=1.5\text{bit}$$

Average Word Length

Let ${\ell }_i$ be the length of the $i$th code, then the average word length $L$ is given by:

$$L=\sum _{i\in \mathcal{I}}{p}_i\cdot {\ell }_i$$

Redundancy

The redundancy is the difference between average word length and entropy (average information content):

$$R=L-H$$

To get the dimensionless relative redundancy $r$, compute:

$$r=\frac{R}{L}$$

---

Types of Codes

Block Codes

Block code means that all codes have equal length, e.g.:

0101010
1000101
1101111
0000000

Linear Codes

Linear code means that you can choose a pair of two codes and their XOR result is again a valid code, e.g.:

0101010
1000101
1101111
0000000

Cyclical Codes

Cyclical code means that you can choose one possible code and shift it by 1 (to left or right) and the result is again a valid code, e.g.:

0101010
1010100
0010101