Cumulative Distribution Function

probability-theory

Definition

Cumulative Distribution Function

The cumulative distribution function $F$ of a random variable $X$ (continuous or discrete) is defined as:

$$F(x)=P(X\le x)\forall x\in \mathbb{R}$$

Properties:

• $F$ is bounded, i.e.: $\forall x\in \mathbb{R}:0\le F(x)\le 1$
• $F$ is monotonically increasing, i.e.: $\forall x,y\in \mathbb{R}:x\le y⟹F(x)\le F(y)$
• $F$ is right-continuous: $\forall x\in \mathbb{R}:{\lim }_{h\to 0+}F(x+h)=F(x)$
• Left/right asymptotes are: ${\lim }_{x\to -\infty }F(x)=0\wedge {\lim }_{x\to +\infty }F(x)=1$

Discrete vs Continuous

Discrete

The cumulative distribution function $F$ is a step function for discrete random variable.

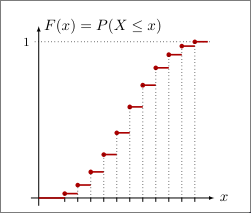
Let $X$ be a discrete random variable taking values $x_1,x_2,\dots$ with pmf $f$ and cumulative distribution function $F$, then:

$$F(x)=P(X\le x)=\sum _{\begin{array}{c}i=1\\ x_i\le x\end{array}}^{\infty }f(x_i)$$

From that, we get:

$$P(a<X\le b)=F(b)-F(a)$$

Continuous

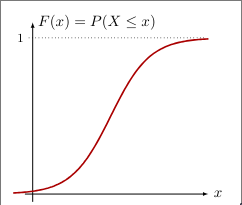
Let $X$ be a continuous random variable with density $f$ and cumulative distribution function $F$, then:

$$F(x)=P(X\le x)={\int }_{-\infty }^{x}f(z)dz$$

From that, we get:

$$P(a<X\le b)=F(b)-F(a)$$

and the density is the cumulative distribution function’s derivative:

$$f(x)=F^{\prime }(x)$$

Inverse

One often needs the inverse function of a cdf $F$. Per definition, $F$ is monotonically increasing, however, there’s no guarantee that $F$ is injective.

Therefore, we need the generalised inverse of $F$.