Knapsack Problem

algorithms

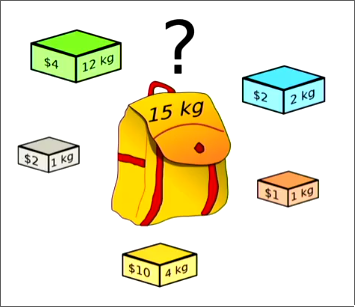
Definition

Knapsack Problem

The Knapsack problem is a problem that asks for filling a fixed-size knapsack with items that have a size and a value such that the total value of the knapsack is maximised. Greedy algorithms on the value of the elements won’t work here.

The Knapsack problem is an optimisation problem is about maximising

$$\sum _{i=1}^n{w}_i{x}_i$$

whereby

$$\sum _{i=1}^n{g}_i{x}_i\le G$$

where $w_i$, is the value and $g_i$ of item $i$, $G$ is the maximum weight capacity of the knapsack, and

$$x_i=\{\begin{array}{ll}1& \text{if item }i\text{ is chosen}\\ 0& \text{if item }i\text{ is not chosen}\end{array}$$

Approaches

Naive Enumeration

Time Complexity: $O(2^n)$ (can’t really be improved generally speaking)

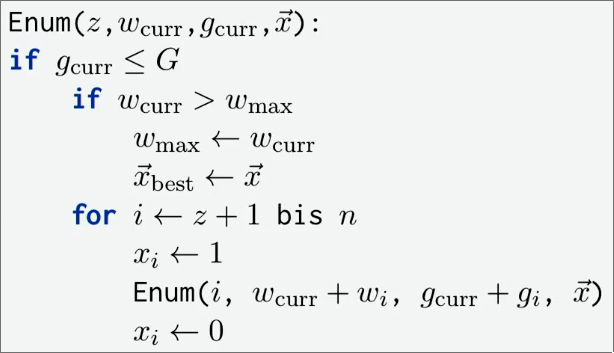
Branch and Bound

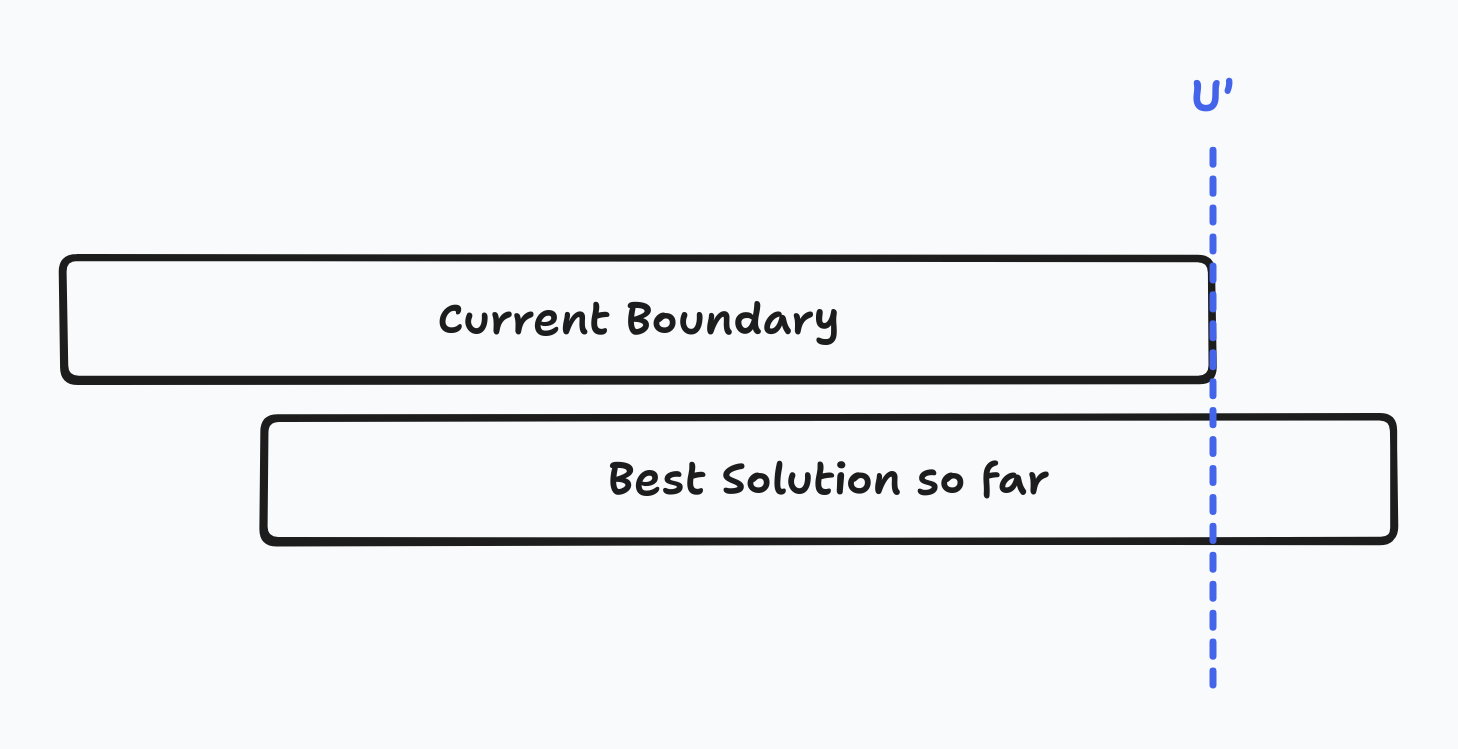
Branch and bound is used here to omit certain subtrees in search space that are not expected to increase the current optimum under the assumption of monotonicity.

If $U^{\prime }\le w_{max}$, then we cannot find any better solution that the current best solution.

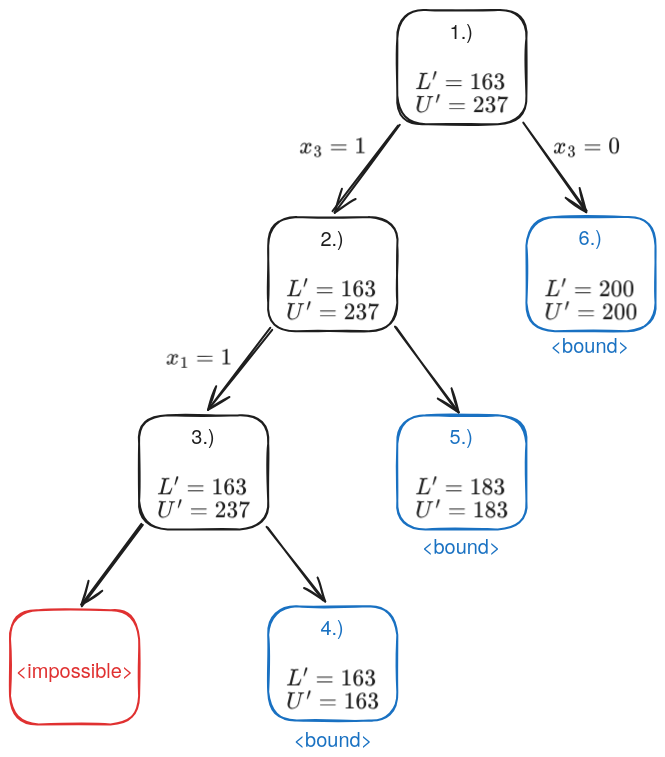
Example: Given $n=4$ items and a knapsack with capacity $G=100$.

Item	1	2	3	4
Weight $g_i$	32	16	21	50
Value $w_i$	80	20	63	100
Coefficient $\frac{w_i}{g_i}$	2.5	1.25	3	2

Order the items according to their coefficients:

1. Item $3$ with $\frac{w_3}{g_3}=3$
2. Item $1$ with $\frac{w_1}{g_1}=2.5$
3. Item $4$ with $\frac{w_4}{g_4}=2$
4. Item $2$ with $\frac{w_2}{g_2}=1.25$

Enumerate $i=3$:

1. Select $i=3$ given that $g_3=21\le 100=G$.
   1. $G^{\prime }=21$ (total weight for current enumeration)
   2. $R^{\prime }=G-G^{\prime }=100-21$ (rest capacity for current enumeration)
   3. $L^{\prime }=63$
   4. $U^{\prime }=63$
2. Select $i=1$ given that $g_3+g_1=21+32=53\le 100$
   1. $G^{\prime }=21+32=53$
   2. $R^{\prime }=G-G^{\prime }=100-53=47$
   3. $L^{\prime }=63+80=143$
   4. $U^{\prime }=63+80=143$
3. Can’t selected $i=4$ given that $g_3+g_1+g_4=21+32+50=103\nleqq 100=G$:
   1. $G^{\prime }=21+32=53$ (remains the same)
   2. $R^{\prime }=G-G^{\prime }=100-53=47$ (remains the same)
   3. $L^{\prime }=63+80=143$ (remains the same)
   4. $U^{\prime }=63+80+\frac{47}{50}\cdot 100=237$
4. Select $i=2$ given that $g_3+g_1+0\cdot g_4+g_2=21+32+16=69\le 100=G$
   1. $G^{\prime }=21+32=53$ (remains the same)
   2. $R^{\prime }=G-G^{\prime }=100-53=47$ (remains the same)
   3. $L^{\prime }=63+80+20=163$
   4. $U^{\prime }=63+80+\frac{47}{50}\cdot 100=237$ (remains the same)
5. Effects:
   • $L^{\prime }=163$
   • $U^{\prime }=237$
   • $L=163$ (best solution so far)
   • $U=237$ (best solution so far)

Observation

As soon as the first item $i^{\prime }$ is found that does not fit inside the knapsack in the current enumeration, i.e. $G^{\prime }+g_{i^{\prime }}>G$, the current capacity $G^{\prime }$, the rest capacity $R^{\prime }$, and the upper bound are fixed. After that, only the lower bound could be adjusted, where possible.

Enumerate: What if $i=3$ is chosen?

• This is equivalent to the enumeration $i=3$ above. Thus:
• Effects:
  • $L^{\prime }=163$
  • $U^{\prime }=237$
  • $L=163$
  • $U=237$

Enumerate: What if $i=3$ and $i=1$ are chosen?

• This is equivalent to the enumeration $i=3$ above. Thus:
• Effects:
  • $L^{\prime }=163$
  • $U^{\prime }=237$
  • $L=163$
  • $U=237$

Enumerate: What if $i=3$, $i=1$, $i=4$ are chosen?

• This is the first occurrence that differs from the enumerations above since $i=4$ were not chosen since it didn’t fit into the Knapsack’s capacity.
• Therefore, this state (and its subsequent subspace) can be ignored.

Enumerate: What if $i=3$, $i=1$ are chosen, but $i=4$ is not chosen?

• In the first enumeration, we tried to put $\frac{47}{50}\cdot 100$ into the Knapsack’s upper boundary. Now, we don’t put $i=4$ into the knapsack at all. Thus:
• Effects:
  • $L^{\prime }=163$ (unchanged)
  • $U^{\prime }=163$ (updated)
  • $L=163$ (unchanged)
  • $U=237$ (unchanged)
• Bound:
  • Given that $L^{\prime }=U^{\prime }=163$, we already found the best solution in the current sub-state space. Further solutions in the current sub-state space don’t need to be explored.

Enumerate: What if $i=3$ is chosen, but $i=1$ is not chosen?

1. Select $i=3$ given that $g_3=21\le 100=G$.
   1. $G^{\prime }=g_3$ (total weight for current enumeration)
   2. $R^{\prime }=G-G^{\prime }=100-21=79$ (rest capacity for current enumeration)
   3. $L^{\prime }=w_3=63$
   4. $U^{\prime }=w_3=63$
2. Next item would be $i=1$, however, we decided to omit it.
3. Select $i=4$ given that $g_3+g_4=21+50=71\le 100=G$
   1. $G^{\prime }=21+50=71$
   2. $R^{\prime }=G-G^{\prime }=100-71=29$
   3. $L^{\prime }=w_3+w_4=63+100=163$
   4. $U^{\prime }=w_3+w_4=63+100=163$
4. Select $i=2$ given that $g_3+g_4+g_2=21+50+16=87\le 100=G$
   1. $G^{\prime }=21+50+16=87$
   2. $R^{\prime }=100-(21+50+16)=13$
   3. $L^{\prime }=w_3+w_4+w_2=63+100+20=183$
   4. $U^{\prime }=w_3+w_4+w_2=63+100+20=183$
   5. We do not add any fraction to $U^{\prime }$ given that there are no more elements that could be added.
5. Effects:
   1. $L^{\prime }=183$
   2. $U^{\prime }=183$
   3. $L=183$ (updated)
   4. $U=237$ (unchanged)
6. Bound:
   1. Again, given that $L^{\prime }=U^{\prime }=183$, we can bound here. There’s no better solution in the current sub-state space.

Enumerate: What if $i=3$ is not chosen?

1. First item would be $i=3$, however, we decided to omit it.
2. Select $i=1$ given that $g_1=32\le 100=G$:
   1. $G^{\prime }=32$
   2. $R^{\prime }=G-G^{\prime }=100-32=68$
   3. $L^{\prime }=w_1=80$
   4. $U^{\prime }=w_1=80$
3. Select $i=4$ given that $g_1+g_4=32+50=82\le 100=G$
   1. $G^{\prime }=32+50=82$
   2. $R^{\prime }=G-G^{\prime }=100-82=18$
   3. $L^{\prime }=w_1+w_4=80+100=180$
   4. $U^{\prime }=w_1+w_4=80+100=180$
4. Select $i=2$ given that $g_1+g_4+g_2=32+50+16=98\le 100=G$
   1. $G^{\prime }=32+50+16=98$
   2. $R^{\prime }=G-G^{\prime }=100-98=2$
   3. $L^{\prime }=w_1+w_4+w_2=80+100+20=200$
   4. $U^{\prime }=w_1+w_4+w_2=80+100+20=200$
   5. Again, no fraction is added to $U^{\prime }$ given that no further items are available to be selected.
5. Effects:
   1. $L^{\prime }=200$
   2. $U^{\prime }=200$
   3. $L=200$ (updated)
   4. $U=200$ (updated)
6. Bound:
   1. Again, given that $L^{\prime }=U^{\prime }$, the best possible solution in the current sub-state space is found. No further exploration needed.

The entire search space is now explored. The most optimal solution is:

• $L=200$
• $U=200$
• $I=\{1,4,2\}$ ($i=3$ is omitted)

Dynamic Programming

The knapsack problem is a classic example for using dynamic programming for a problem. Given $n$ items, where each item has a size and a value, you try to solve all sub-problems for $i=n-1,n-2,\dots$. During solving this problem, a table is built:

$i/w$	0	1	2	…	$w$
0	0	0	0	…	0
1				…
2				…
…	…	…	…	…	…
$n$				…

After the DP table is built, the algorithm just chooses based on the table dp[n][max_size].

TL;DR: Dynamic Programming Approach

The dynamic programming approach solves the problem for all $0\le i\le n$ and $0\le w\le \text{max\_size}$, builds up a table and picks the solution for the desired problem.

Solutions of smaller problems can be used for the next bigger problem, until the desired problem is picked.

Python:

def knapsack(max_size: int, items: list[tuple[int, int]]) -> int:
	n: int = len(items)
	dp: list[list[int]] = [
		[0] * (max_size + 1)
		for _ in range(n + 1)
	]
	for i in range(1, n + 1):
		item_size, item_value = items[i - 1]
			for w in range(max_size + 1):
				if item_size <= w:
					dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - item_size] + item_value)
				else:
					dp[i][w] = dp[i - 1][w]
	return dp[n][max_size]