Law of Large Numbers

statistics

Definition

Law of Large Number

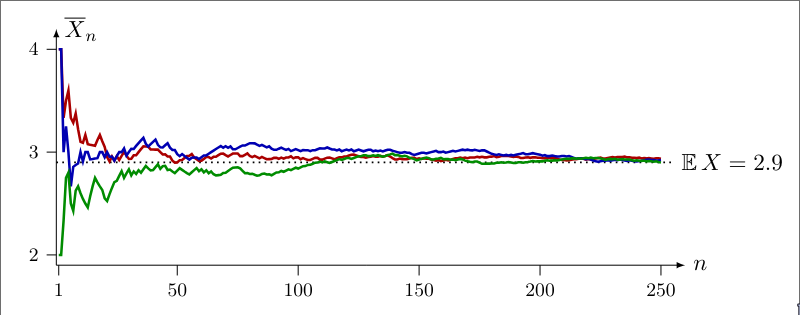
The Law of Large Numbers states that the sample mean $\overline{X_n}$ will be - with high probability - very close to the expectation of the underlying distribution.

Let $X_1,X_2,\dots$ be a sequence of identically distributed random variables with finite variance:

$$\mathbb{V}ar(X_i)={\sigma }^2<\infty \forall i\in \{1,2,\dots ,n\}$$

where $P$ is the probability measure. Denote the sample mean of the first $n$ random variables by $\overline{X_n}$, then:

$$\forall \epsilon >0:\underset{n\to \infty }{\lim }P(\left|\overline{X_n}-\mathbb{E}[X_i]\right|<\epsilon )=1$$

In other words, the sample mean of an identically distributed random variable with finite variance converges in probability to the mean $\overline{X_n}\stackrel{p}{\to }\mathbb{E}[X_i]$.