Offset Binary

numeric

Definition

Offset Binary

Offset Binary is a method for signed number representation where a signed number n is represented by the bit pattern corresponding to the unsigned number $n+k$, $k$ being the biasing value or offset.

¹

Symmetry

There are two types of offset binary: symmetric and asymmetric offset.

Symmetric Offset

The Symmetric offset adds a single constant excess to all numbers:

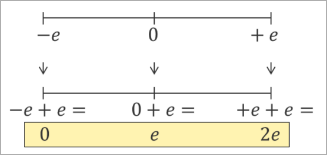
The goal is to represent negative numbers as positive numbers. They don’t need to be stored as signed numbers. Thus, all numbers $n$ are representable by an excess $e$ if $n\in [-e,e]$.

The excess is derived from the smallest representable negative number:

$$0_e=e$$

Example: $e=4$

Actual Value	Calculation	Offset Binary Code	Binary Representation
-4	-4 + 4 = 0	0	000
-3	-3 + 4 = 1	1	001
-2	-2 + 4 = 2	2	010
-1	-1 + 4 = 3	3	011
0	0 + 4 = 4	4	100
1	1 + 4 = 5	5	101
2	2 + 4 = 6	6	110
3	3 + 4 = 7	7	111

For an unsigned bit pattern of bit length $m$, the excess is always:

$$e=2^m$$

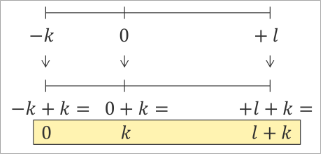
Asymmetric Offset

Arithmetic

Addition

Let $e$ b the excess, and $A_e=A+e$ and $B_e=B+e$, adding these two excess-numbers is equal to:

Wrong:

$$A_e+B_e=(A+e)+(B+e)=A+B+\underset{\text{Must be e}}{\underbrace{2e}}$$

Correct:

$$\begin{array}{rl}{A}_e+B_e=(A+B{)}_e& =A+B+e\\ & =A_e+B\\ & =A+B_e\\ & =A_e+B_e-e\end{array}$$

Footnotes

1. Offset binary - Wikipedia ↩