Floating-Point Number Representation

numeric

Definition

Floating-Point Number Representation

The floating-point number representation is a method of representing decimal numbers on the computer.

Exponent Notation

The foundation for understanding floating-point numbers is the exponent notation. Decimal numbers can be represented as follows:

$$x=m\cdot b^e$$

where:

• $x$ is the decimal number to be represented
• $m$ is the mantissa
• $e$ is the exponent
• $b$ is the basis

Clearly, this notation does not have a single unique representation for all decimal numbers. For example: $0.00123=123\cdot 10^{-5}=12.3\cdot 10^{-4}$. Thus, the notation must be normalised in order to have a single valid representation in the memory.

There must be a single digit directly before the command, and the single digit must not be 0 for binary representation. Now, the representation of the above example is more clear:

$$0.00123=1.23\cdot 10^{-3}$$

Remark

Notice that we postulated that the pre-comma digit of the mantissa must not be zero. Therefore, in the binary system, the only other possible digit is 1. Using that knowledge, less information has to be stored.

Layout

The first bit denotes the sign of the represented number, where:

• 0 means positive, and
• 1 means negative.

The mantissa is represented as fixed-point number with exact one pre-comma digit.

---

IEEE754

The following floating-point number system can represent numbers between $[e_{min}-1,e_{max}+1]$.

$$\mathbb{F}(b,p,e_{min},e_{max},\text{denorm})$$

The excess is relative to the smallest representable number:

$$e=-e_{min}+1$$

IEEE754 Conventions

Some values have fixed representatios:

• Zero:
  • Sign: 0 or 1
  • Exponent Bits: all set to 0
  • Mantissa: all set to 0
• NaN:
  • Sign: 0
  • Exponent Bits: all set to 1
  • Mantissa: at least one bit is not 0
• Plus Infinity:
  • Sign: 0
  • Exponent Bits: all set to 1
  • Mantissa Bits: all set to 0
• Minus Infinity:
  • Sign: 1
  • Exponent Bits: all set to 1
  • Mantissa Bits: all set to 0

Conversion

Converting to Normalised Numbersj

Example: Converting $(-172.625{)}_{10}$ into IEEE754 Single Precision:

$$\text{IEEE754 Single Precision}\widehat{=}\mathbb{F}(2,24,-126,+127,true)$$

1. Step: Convert $(-172.625{)}_{10}$ into the binary number system:

$$\begin{array}{rl}(-172{)}_{10}& =(-10101100{)}_2\\ (0.625{)}_{10}& =(0.101{)}_2\\ & \\ ⟹(-172.625)& =(-10101100.101{)}_2\end{array}$$

1. Step: Normalise $(-1\underset{7\text{bits}}{\underbrace{0101100}}{)}_2=(-1.0101100101)\cdot 2^7$

2. Step: Offset exponent $(7{)}_{10}=(110{)}_2$ with excess $(127{)}_{10}=(01111111{)}_2$:

$$\begin{array}{rl}& 01111111\\ +& 00000111\\ & \\ =& 10000110\end{array}$$

1. Step: Layout:

$$\underset{1}{\underbrace{1}}\underset{8}{\underbrace{10000110}}\underset{1}{\underbrace{1}}\underset{23}{\underbrace{01011001010000000000000}}$$

The implicit bit ($1$, red) can be omitted since it will always be $1$. Thus, the layout is:

$$\underset{1}{\underbrace{1}}\underset{8}{\underbrace{10000110}}\underset{23}{\underbrace{01011001010000000000000}}$$

The result is a 32 bit word. The least significant bit $1$ (cyan) signals that the number if negative.

---

Rounding

Rounding is important in numeric since computers can only store a certain number of bits, meaning a limited precision. There are multiple methods of rounding for floating point numbers.

Truncate

Truncating means removing a part of or the whole fractional part from a number.

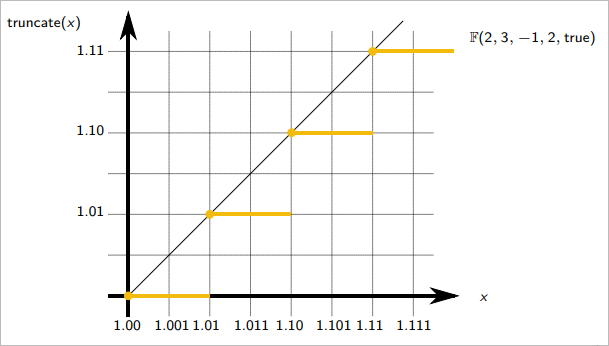
Example: Truncating $(-1.626{)}_{10}$ to 2 decimal digits is $(-1.62{)}_{10}$.

Directed Rounding

Directed rounding refers to rounding an number in a specific direction:

1. Round Towards Zero: Always rounds the number closer to zero.
2. Round Away from Zero: Always rounds the number farther from zero.

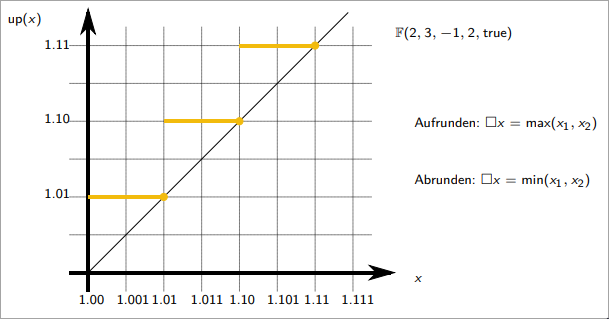
Examples:

• Rounding Towards Zero: $\text{down}((1.524{)}_{10})=(1.52{)}_{10}$
• Round Away from Zero: $\text{up}((1.524{)}_{10})=(1.53{)}_{10}$

Round to Nearest

Rounding to the nearest refers to rounding a number to the closest value at a specified level of precision, such as the nearest integer, tenth, hundredth, or any other place value.

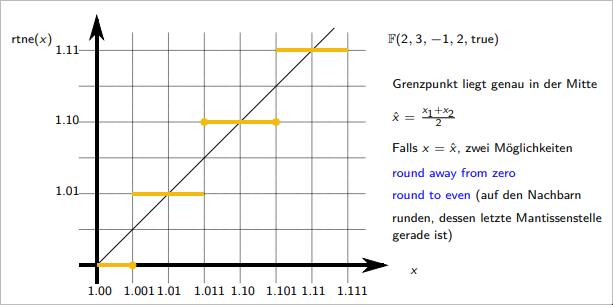
Precision of Rounding

Arithmetic

Addition

todo

Subtraction

todo

Multiplication

todo

Division

todo