Turing Machine

computation

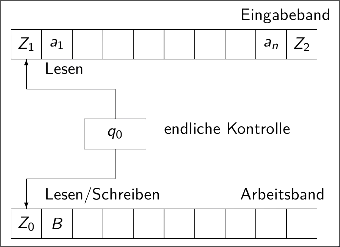
Definition

Turing Machine (Standard)

A Turing machine consists of seven components:

$$M=⟨Q,\Sigma ,\Gamma ,\delta ,q_0,B,F⟩$$

where:

• $Q$ is a finite set of states.
• $\Sigma$ is the input alphabet.
• $\Gamma$ is the tape alphabet.
• $\delta :Q\times \Sigma \to Q\times \Gamma \times D$ is a transition function.
• $D=\{L,R,S\}$ (left, right, stay) is the direction in which the head should move.
• $q_0\in Q$ is the initial state.
• $B\in \Gamma \setminus \Sigma$ is the blank symbol.
• $F\subseteq Q$ are the accepting) states.

A Turing machine halts on the first occasion of a final state $f\in F$.

Turing Machine (Boundary Symbols)

A Turing machine consists of eight components:

$$M=⟨Q,\Sigma ,\Gamma ,\delta ,q_0,\{Z_0,Z_1,Z_2\},B,F⟩$$

where:

• $Q$ is a finite set of states.
• $\Sigma$ is the alphabet of the input tape.
• $\Gamma$ is the alphabet of the working tape.
• $\delta :Q\times \Sigma \times \Gamma \to Q\times \Gamma \times D_i\times D_w$ is a transition function
• $D_H=\{L,R,S\}$ (left, right, stay) is the direction in which the head $H$ should move.
• $q_0\in Q$ is the initial state.
• $Z_0\in \Gamma$ is the left boundary symbol on the working tape
• $Z_1$ is the left boundary symbol on the input word
• $Z_2$ is the right boundary symbol on the input word
• $B\in \Gamma \setminus \Sigma$ is the blank symbol.
• $F\subseteq Q$ are the accepting) states.

A Turing machine halts on the first occasion of a final state $f\in F$.

Tape

Definition

Tape (Turing Machine)

A tape is an infinite sequence of elements where each element can be blank $B$ or a state $X_i\in Q$. Almost all cells are non-blank.

Link to original

Configuration

Definition

Configuration (Turing Machine)

A configuration is a complete snapshot of a Turing machine at a single moment.

Move to left, i.e.: $\delta (q,X_i)=(p,Y,\underline{L})$:

$$X_1{X}_2\dots X_{i-1}q{X}_i{X}_{i+1}\dots X_n⟹X_1{X}_2\dots X_{i-2}p{X}_{i-1}Y{X}_{i+1}\dots X_n$$

Move to right, i.e.: $\delta (q,X_i)=(p,Y,\underline{R})$:

$$X_1{X}_2\dots X_{i-1}q{X}_i{X}_{i+1}\dots X_n⟹X_1{X}_2\dots X_{i-1}Yp{X}_{i+1}{X}_{i+2}\dots X_n$$

Move stays (no movement), i.e.: $\delta (q,X_i)=(p,Y,\underline{S})$:

$$X_1{X}_2\dots X_{i-1}q{X}_i{X}_{i+1}\dots X_n⟹X_1{X}_2\dots X_{i-1}pY{X}_{i+1}\dots X_n$$

Link to original

Language

Accepted Language

Accepted Language (Turing Machine)

The accepted language $\mathcal{L}(M)$ of a Turing machine $M$ are all words for which $M$ terminates:

$$\mathcal{L}(M)=\{w\in {\Sigma }^{\ast }\mid q_{0}w⟹\alpha p\beta ,p\in F,\alpha ,\beta \in {\Gamma }^{\ast }\}$$

Recursive Enumerable Language

Definition

Recursively Enumerable Language

A language $\mathcal{L}\subseteq {\Sigma }^{\ast }$ is recursively enumerable if there exists a Turing machine $M$ such that:

1. for every $w\in \mathcal{L}$, $M$ halts and accepts $w$,
2. for every $w\notin \mathcal{L}$, $M$ either rejects or runs forever.

i.e., there exists a Turing machine that accepts $L$.

Equivalently, there’s a program that enumerates all strings of $\mathcal{L}$ (possibly with repetition) $w_1,w_2,\dots$, every member of $\mathcal{L}$ appears after finite time.

Link to original

Recursive Language

Definition

Recursive Language

A language $\mathcal{L}\subseteq {\Sigma }^{\ast }$ is recursive (or decidable) if there exists a total Turing machine $M$ such that, for every input $w\in {\Sigma }^{\ast }$, $M$ halts and:

1. if $w\in \mathcal{L}$, $M$ accepts $w$;
2. if $w\notin \mathcal{L}$, $M$ rejects $w$.

Equivalently:

• The characteristic function ${\chi }_{\mathcal{L}}:{\Sigma }^{\ast }\to \{0,1\}$ is computable.
• Both $\mathcal{L}$ and its complement $\overline{\mathcal{L}}$ are recursively enumerable.
• There exists a program that, given any string $w$, decides membership in finite time.

Link to original

Deterministic

Definition

Deterministic Turing Machine

A Turing machine $M$ is called deterministic, if for all $(q,X)\in Q\times \Gamma$ there exists at most one element $(q,X;p,Y,D)\in \delta$, i.e.:

$$\forall (q,X)\in Q\times \Gamma :\left|\{(q,X;p,Y,d)\mid p\in Q,Y\in \Gamma ,d\in D\}\right|\le 1$$

with $D\in \{L,R,S\}$. Denote $\delta (q,X)=(p,Y,D)$.

Link to original

Computation

Computation of an Arithmetic Function

Denote $[n{]}_2$ as the binary representation of an $n\in \mathbb{N}$. The initial configuration of a Turing machine $M$ with alphabet $\Sigma =\{0,1\}$. The input works on input:

$$(n_1,n_2,\dots ,n_k)\in {\mathbb{N}}^k\cong ([n_1{]}_2,[n_2{]}_2,\dots ,[n_k{]}_2)\in ({\Sigma }^{+}{)}^k$$

where ${\Sigma }^{+}$ must not contain leading zeros.

The initial configuration of $M$ is where $B$ (blank symbol) separates each block.

$$q_0[n_1{]}_{2}B[n_2{]}_{2}B\dots B[n_k{]}_2$$

Example Initial Configuration

Let $k=3$ and $(n_1,n_2,n_3)=(5,2,7)$ with binaries $(101,10,1111)$. Here, the initial configuration is:

$$q_{0}101B10B1111$$

The end configuration of a (function-computing) Turing machine $M$ is given by:

$$xp[n{]}_{2}By$$

with $p\in F$ (final state), $x,y\in {\Gamma }^{\ast }$ (tape words), and $M$ emits $n\in \mathbb{N}$.

Parsing " $xp[n{]}_{2}By$"

• The head is position at the leftmost bit because $p\in F$ (final state) precedes $[n{]}_2$.
• Right after the number there is a blank $B$ (a delimiter).
• The machine is in an accepting (final) state $p$, i.e., it has halted.
• Therefore, the output is $n$.

$x,y\in {\Gamma }^{\ast }$ is arbitrary content elsewhere. It doesn’t matter what’s left in $x$ or $y$.

Computation of $f:{\mathbb{N}}^k\to \mathbb{N}$

A Turing machine $M$ with input alphabet $\Sigma =\{0,1\}$ computes an arithmetic function $f:{\mathbb{N}}^k\to \mathbb{N}$ if $M$ works on $(n_1,\dots ,n_k)$ as input, and outputs $f(n_1,\dots ,n_k)$. Denote $F(M)=f$.

Example with input $6$

Let $M=(\{q_0,q_1,q_2\},\{0,1\},\{0,1,B\},\delta ,q_0,B,\{q_2\})$. Let $\delta$ be:

State/Input	$0$	$1$	$B$
$q_0$	$(q_0,0,R)$	$(q_0,1,R)$	$(q_1,0,S)$
$q_1$	$(q_1,0,L)$	$(q_1,1,L)$	$(q_2,B,R)$

For instance, let $6$ be the input. Thus, the tape contains $[6{]}_2=110$:

$$\begin{array}{rl}{q}_{0}110& ⟹1q_{0}10⟹11q_{0}0⟹110q_0[B]⟹110q_{1}0\\ ⟹11q_{1}00& ⟹1q_{1}100⟹q_{1}1100⟹q_{1}B1100⟹q_{2}1100\end{array}$$

The Turing machine halts at $q_2\in F$. The output is $1100=[12{]}_2$, see final configuration.

The computed function is $f_1=F(M):\mathbb{N}\to \mathbb{N}$, whereby $f_1(n)=2n$.

Note: The same Turing machine $M$, applied on number pairs, computes $f_2=f(M):{\mathbb{N}}^2\to \mathbb{N}$, whereby:

$$f_2(m,n)=m\cdot 2^{bl(n)+1}+n$$

where $\mathrm{bl}$ is the binary length:

$$\begin{array}{rl}\mathrm{bl}(0)& =1\\ \mathrm{bl}(k+1)& =\lfloor {\log }_2(k+1)\rfloor +1\end{array}$$