Type-i Grammar

languages

Definition

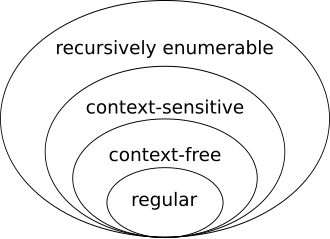
Type 0

Definition

Grammar

A grammar $G$ is a 4-tuple:

$$G=⟨N,T,P,S⟩$$

where:

• $N$ is the finite set of non-terminal symbols
• $T$ is the finite set of terminal symbol ($N\cap T=\{\}$)
• $P\subseteq (N\cup T{)}^{+}\times (N\cup T{)}^{\ast }$ are the product rules
• $S\in N$ is the start symbol

Denote:

• $\alpha \to \beta$ instead of $(\alpha ,\beta )\in P$
• $\alpha \to {\beta }_1|\dots |{\beta }_n$ instead of $\alpha \to {\beta }_1,\dots ,\alpha \to {\beta }_n$

Further, $G$ is also called unconstrained grammar or type- grammar.

Link to original

Type 1

Definition

Context-Sensitive Grammar (Type-1)

A grammar $G=(N,T,P,S)$ is called context-sensitive (Type-1) if every production in $P$ is of the form $\alpha \to \beta$ where there exist $u,v\in (N\cup T{)}^{\ast }$, $A\in N$, and $w\in (N\cup T{)}^{+}$ such that

$$\alpha =uAv\text{and}\beta =uwv.$$

In words: a single nonterminal $A$ may be replaced by a nonempty string $w$, but only in its surrounding context $u\_\square v$.

Link to original

Type 2

Definition

Context-Free Grammar (Type-2)

A grammar $G=(N,T,P,S)$ is called context-free (Type-2) if every production in $P$ is of the form

$$A\to \beta$$

where $A\in N$ and $\beta \in (N\cup T{)}^{\ast }$.
That is, the left-hand side of every production consists of a single nonterminal.

A language is called context-free there exists a pushdown automaton that accepts it.

From the start symbol, non-terminal symbols are iteratively replaced by applying the respective production rules.

Link to original

Type 3

Definition

Regular Grammar (Type-3)

A grammar $G=(N,T,P,S)$ is called regular (Type-3) if every production in $P$ is of one of the forms

$$A\to aB\text{or}A\to \epsilon$$

where $A,B\in N$, $a\in T$, and $\epsilon$ is the empty word.
Such a grammar (right-linear) generates exactly the regular languages.

Link to original